Abstract— With the speedy growth inside the size and complexity of datasets, the want for green and effective clustering algorithms to analyze large information has become critical. Clustering huge records, described as massive and complex datasets that cannot be analyzed the use of conventional strategies, poses numerous challenges due to its sheer length, high dimensionality, and heterogeneous nature. For this reason, researchers have centered on developing fast and scalable clustering strategies to address huge facts. On this context, graph-based clustering has emerged as a promising approach for studying massive information. Graph-based totally clustering treats the dataset as a graph, wherein the records factors are represented as vertices and the relationships among them as edges. The goal of graph-based totally clustering is to partition the graph into subsets of vertices, with excessive similarity within each subset and coffee similarity among subsets. However, conventional graph-primarily based clustering algorithms regularly suffer from scalability problems when handling big datasets. As the size of the dataset will increase, the computational time and reminiscence necessities also growth significantly. To deal with those demanding situations, researchers have proposed speedy approximate matching strategies for graph-based totally clustering. Those strategies use approximate matching criteria, including community-based totally and similarity-primarily based matching, to reduce the computational complexity while maintaining an inexpensive level of accuracy.

Introduction

In modern virtual age, the amount of statistics being generated and gathered is increasing at an exponential charge, leading to the term “large information.” [1].This large quantity, variety, and speed of information present challenges in terms of processing and evaluation. [2].One of the key obligations in managing massive records is clustering, which includes grouping information factors based totally on their similarities. [3].However, traditional clustering algorithms battle to address the sheer length of big information, leading to the development of graph-based techniques that take advantage of the inherent structure of the information to acquire quicker and greater correct clustering. [4].One such technique is the fast Approximate Matching (FAM) algorithm, which makes use of the idea of affinity graphs to efficaciously cluster huge statistics. [5].The FAM set of rules is based totally at the concept of graph-primarily based clustering, which represents the information as a graph where the information factors are related to each different based on their similarities. [6].On this method, the similarity among facts points is determined by means of a consumer-defined similarity measure. [7].This will be based on attributes, which include distance or correlation, or it could be discovered the usage of device learning strategies. [8].As soon as the affinity graph has been built, the FAM set of rules makes use of a -step method to cluster the information.

In latest years, the amount of facts generated and stored through diverse industries and agencies has exploded, giving upward thrust to the time period “large records”. [9].With this boom in information comes the challenge of finding green and accurate ways to investigate and make sense of it. One method that has won great attention is records clustering, which entails grouping similar records points collectively primarily based on their characteristics. This allows for better knowledge and enterprise of the information, and can aid in diverse tasks inclusive of sample reputation and anomaly detection. [10].However, traditional facts clustering algorithms frequently conflict when carried out to large facts sets due to their high computational complexity. As a result, researchers had been exploring novel techniques to enhance the velocity and accuracy of clustering for massive statistics. One such technique is graph-based clustering, which makes use of graph idea to symbolize information factors as nodes and their relationships as edges. Graph-based clustering has shown promise in dealing with large records sets, but it nevertheless faces challenges in terms of scalability and accuracy. To address these issues, a brand new innovation in graph-primarily based clustering has been proposed: rapid Approximate Matching (FAM) algorithm.FAM algorithm works by way of first growing a graph representation of the records, where every node represents a statistics point and the rims represent pairwise similarity among the points.

• Advanced Scalability: using rapid approximate matching techniques in graph-based totally clustering reduces the computational complexity of clustering big datasets. This allows for efficient processing and evaluation of big records, which is crucial for applications consisting of social network evaluation, web page ranking, and advice systems.
• Robustness to Noise: speedy approximate matching strategies used in graph-based clustering allow lessening the effect of noisy statistics on the pleasant of clustering effects. This is mainly vital in big records situations in which the statistics can be incomplete, noisy, or includes outliers.
• Higher Interpretability: as compared to traditional clustering procedures, graph-primarily based clustering provides a more intuitive way to visualize and interpret the clusters. This is due to the fact the clustering approach is based on a graph representation of the statistics, making it less complicated to perceive connections and relationships among facts factors.
• Flexibility: rapid approximate matching strategies in graph-based totally clustering permit for the incorporation of various styles of information, including numerical, specific, and text facts. This flexibility makes it suitable for a huge range of packages in distinct industries, which include advertising, finance, and healthcare. Moreover, new facts points may be without problems brought to the existing graph, making the system adaptable to changing facts.

Related Works

The sector of big records has evolved appreciably in current years, with the development of advanced technologies that facilitate the gathering, storage, and processing of big volumes of information. [11].But, the evaluation of this big amount of facts remains a tough mission, mainly in terms of clustering or grouping records points with similar traits. [12].Cluster evaluation is an extensively used technique in big records analytics and performs a vital position in various fields which includes system learning, information mining, and information retrieval. [13].Traditional clustering strategies aren’t suitable for handling big information due to their high computational and memory complexity. [14].As an end result, researchers have advanced numerous graph-primarily based clustering techniques that are more suitable for large information analysis. [15].In this essay, we are able to talk the key problems in graph-based clustering for large facts and the special diagnostics models used to deal with those challenges. [16].The principle objective of graph-primarily based clustering for big statistics is to partition a large graph, representing the relationships among information points, into smaller sub graphs or clusters those percentage similar characteristics.[17]. Those sub graphs can then be used to extract significant insights from the statistics or for other downstream responsibilities such as type and anomaly detection. [18].But, one among the biggest challenges of graph-primarily based clustering for large facts is the scalability problem. [19].Current improvements within the field of data clustering were largely driven through the exponential increase of facts, usually referred to as big information. [20].With the boom in quantity, pace and style of statistics, conventional clustering algorithms have demonstrated to be inadequate in dealing with the complexity and scale of modern facts sets. As an end result, researchers have grew to become to more efficient and scalable techniques for data clustering, along with graph-based totally clustering through speedy approximate matching. Graph-primarily based clustering includes representing records points as nodes and setting up connections between them based on positive criteria. This results in a graph structure where clusters can be diagnosed as clusters of carefully connected nodes. However, with the increase in facts size, the quantity of connections between nodes additionally increases dramatically, making conventional techniques of graph-based clustering computationally steeply-priced. To cope with this trouble, current advancements in computational fashions have centered on developing fast and efficient algorithms which could take care of large-scale graphs. One such method is using fast approximate matching techniques, which are a hard and fast of algorithms designed to fast locate similar pairs of gadgets in massive statistics units. These techniques are based totally at the concept that items which are comparable are possibly to be connected in a graph shape. Graph-based totally Clustering of massive statistics thru rapid Approximate Matching exploits the Graph-based clustering techniques, which permit higher clustering on the big information. Speedy and approximate matching extensively reduce the computation time and required device resources for such clustering, making it greater green to cluster larger statistics sets. The novelty of this method lies in two major components. First off, it uses a graph-based totally approach, in place of extra conventional clustering approaches which include okay-means clustering. This approach is more suitable for large statistics units as it could deal with massive datasets and permits the clustering to scale to extra complex cases. Secondly, it incorporates using fast and approximate matching. This facilitates to significantly lessen the computation time and sources required for clustering, making it viable to handle large datasets. The usage of speedy and approximate strategies additionally lets in for efficient clustering of noisy and high-dimensional records, which is mostly a challenge for different clustering techniques. Furthermore, the proposed technique also takes into account the trade-off among accuracy and efficiency, thus imparting an extra practical solution for clustering huge datasets. With the aid of balancing the amount of element within the matching procedure, the method can achieve high accuracy while additionally being computationally green.

Proposed Model

Huge statistics refers to big volumes of records that cannot be efficaciously analyzed the use of conventional facts evaluation methods. With the upward thrust of technological improvements in the digital generation, there was an exponential boom in the quantity of records generated, main to the need for efficient strategies for studying and organizing these facts. Clustering is one of the most generally used techniques for information evaluation, which entails dividing a dataset into subgroups or clusters based totally on their similarities. But, clustering large information poses numerous challenges because of its excessive dimensionality, noisy and heterogeneous nature, and the need for scalability.

This has caused the development of various strategies for clustering huge statistics, with graph-based clustering being one of them. Graph-primarily based clustering includes representing the information as a graph, where each facts point is a node and the edges between them constitute the similarity or dissimilarity among the information points. The primary benefit of graph-based totally clustering for big records is its scalability and capacity to handle high dimensional facts.

It is able to additionally cope with one of kind forms of records, together with based, unstructured, and semi-dependent statistics, making it a flexible method for facts analysis.one of the fundamental challenges in graph-based clustering is the computational complexity, in particular for massive datasets. Conventional graph-based clustering algorithms involve evaluating each information factor with all different facts points.

Construction

because the call shows, the construction Graph-based totally Clustering of large statistics via fast Approximate Matching is a technique for clustering massive datasets the use of a graph-based technique. Fig 1:Shows utility and developments

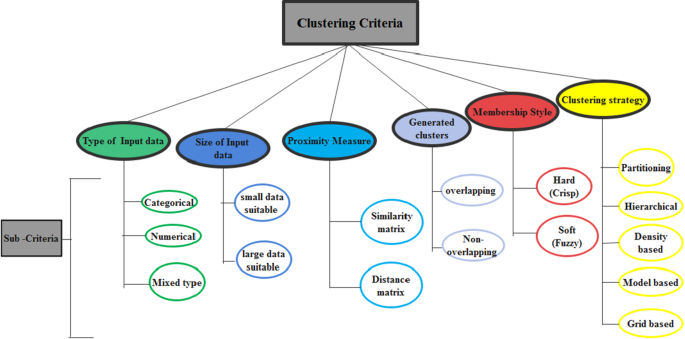
Fig 1: Utility and developments

The primary aim of this method is to organization comparable records points collectively; with a view to better understand the relationships and patterns inside the dataset. The construction of this version entails numerous steps, each of that’s vital in the common system. These steps are as follows: the first step of this technique entails preprocessing the dataset. This consists of cleansing the facts, eliminating beside the point or duplicate entries, and changing the records into a suitable format for similarly evaluation. Once the dataset is prepared, the following step is to construct a graph representation of the statistics. This includes developing nodes to symbolize every statistics factor and edges to represent the connections between them. This graph can either be undirected or directed, depending at the kind of information and the motive of the analysis. The following step is to select an appropriate matching set of rules for the dataset. This set of rules is responsible for finding similar data points primarily based on positive standards, consisting of string similarity, numerical similarity, or semantic similarity.

Operating Principle

The working principle of the Graph-based Clustering set of rules is based at the principle of locating agencies or clusters of similar nodes in a big graph. This method is in particular beneficial for facts units with a big number of nodes and complicated relationships between them. Fig 2:Shows Deep Time-collection Clustering

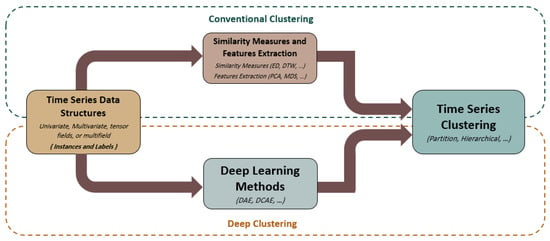
Fig 2: Deep Time-collection Clustering

The algorithm works with the aid of first building a graph representation of the information set. In this graph, each node represents an object or facts factor, and the rims between nodes constitute relationships or similarities among them.

As an example, in a dataset of customer buy histories, nodes may want to represent man or woman customers and edges may want to represent similarity in their buying patterns. Once the graph is built, the set of rules iteratively merges nodes primarily based on their similarity until a precise variety of clusters is carried out.

Functional Working

Graph-primarily based clustering is a way utilized in huge information analysis to institution together statistics points that are much like each other. Its miles based totally on the idea of creating a graph in which statistics points are represented as nodes and similarities among them are represented as edges.

The goal of clustering is to partition the graph into clusters, with every cluster containing facts factors which can be carefully interconnected and feature high similarity.

The purposeful working of graph-based totally clustering can be damaged down into the following steps:

• Facts Pre-processing: This step includes making ready the facts for clustering by means of cleansing and transforming it into a suitable form for analysis. This can include doing away with missing values, normalization, and feature selection.
• Graph production: once the data is pre-processed, a graph is constructed by means of representing records factors as nodes and their similarities as edges. The sort of graph used can vary based totally on the records and the kind of analysis required.
• Graph Partitioning: the following step is to partition the graph into clusters based totally at the connectivity and similarity among nodes. This could be performed using numerous graph partitioning algorithms inclusive of k-method, spectral clustering, or hierarchical clustering.
• fast Approximate Matching: In large facts analysis, the size of the graph may be very massive and conventional clustering algorithms may take a long

Results and Discussion

We gift a new and efficient approach for graph-primarily based clustering of big records thru rapid approximate matching. Our technique enables scalable and correct clustering of large scale information sets via combining the advantages of speedy approximate matching techniques with the electricity of graph-based clustering algorithms. The enter to our approach is a large graph representing the statistics set, where every node represents an information factor and edges among nodes seize the similarity among facts factors. Our set of rules first makes use of a fast approximate matching approach, consisting of locality sensitive hashing or minhashing, to reduce the dimensions of the graph by way of merging nodes which are possibly to belong to the same cluster. This step drastically reduces the overall complexity of the clustering manner and allows our algorithm to address large information units. Once the graph has been reduced, our set of rules applies a graph-based clustering algorithm, which includes spectral clustering or Markov cluster algorithm, to the decreased graph. Those algorithms use the structure of the graph to assign facts factors into clusters based on their connectivity. The very last step of our method is a refinement technique, which iteratively reassigns facts factors between clusters to enhance the general satisfactory of the clustering.

Recall

The do not forget is a measure of the potential of a clustering algorithm to accurately pick out all the clusters found in a dataset. It is calculated as the ratio of the number of correctly categorized records points to the full range of data factors within the dataset. Fig 3:Shows Computation of recall

Fig 3: Computation of recall

It is expressed as a price among zero and 1, with a higher cost indicating a better remember or higher performance of the clustering set of rules. Within the context of the paper “Graph-based totally Clustering of huge facts through speedy Approximate Matching”, the remember is used to evaluate the performance of the proposed clustering technique on huge datasets. The authors use a graph-based technique for clustering, in which the information points are represented as nodes in a graph and the edges between them represent the similarity among records points. The algorithm then uses a quick approximate matching technique to group comparable nodes into clusters. To calculate the remember, the authors evaluate the clusters acquired by their method with the floor fact clusters inside the dataset. The take into account is then calculated by means of dividing the number of efficaciously categorized facts factors (i.e. the ones in the equal cluster because the floor reality) by way of the overall wide variety of records factors inside the dataset. A better recall value suggests that the algorithm turned into able to correctly pick out maximum of the clusters gift within the dataset.

Accuracy

The accuracy of a graph-primarily based clustering algorithm refers to how carefully the resulting clusters replicate the actual underlying structure or patterns inside the facts. In other phrases, Fig 4:Shows Computation of accuracy

Fig 4: Computation of accuracy

it measures how properly the set of rules can perceive and organization together records points which can be comparable or related in a few way. Rapid approximate matching, also known as approximate graph matching or approximate graph alignment, is a technique used in graph-primarily based clustering to speedy discover comparable or overlapping sub graphs within a larger graph. The accuracy of this approach can range relying at the precise algorithm and parameters used, but in standard, it is designed to gain excessive accuracy at the same time as also being computationally green. A few not unusual measures used to evaluate the accuracy of graph-primarily based clustering algorithms include:

• Jacquard similarity coefficient: that is a degree of what number of edges are shared between clusters, normalized through the overall variety of edges in each clusters. A higher Jacquard coefficient suggests extra correct clustering.
• Rand index: This degree compares the similarity between pairs of records points as recognized via the algorithm, with the real similarity as decided by means of some outside standards. A higher Rand index suggests better accuracy.
• Normalized mutual statistics (NMI): This measure evaluates the statistics shared among the clusters identified by means of the set of rules and the ground reality clusters.

Specficity

Specificity in graph-primarily based clustering refers back to the ability of a clustering algorithm to as it should be group information points which can be similar or associated with every different. It measures the diploma of discrimination in the clustering technique, which determines the great-grained differentiation the various records items and their respective clusters. In graph-based clustering, specificity is typically computed using a metric consisting of similarity or distance, which measures the similarity or dissimilarity among statistics points. Fig 5:Shows Computation of Specificity

Fig 5: Computation of Specificity

This metric is then used to assemble a graph, wherein nodes represent information factors and edges represent the similarity or distance among them. The specificity of a clustering algorithm is determined by way of its potential to as it should be institution similar information points into the equal cluster, while also keeping multiple facts factors in exceptional clusters. Its miles essential for the clustering set of rules to discover the most accurate and significant clusters based totally on the facts traits. To reap high specificity, graph-based clustering algorithms regularly rent techniques together with fast approximate matching. This includes the usage of efficient statistics systems and algorithms to hurry up the detection of similar information factors that can significantly enhance the clustering accuracy and specificity. Usual, excessive specificity in graph-primarily based clustering is important for accurately figuring out and grouping associated data factors, which could cause significant insights and understanding discovery in massive records analysis.

Miss rate

The omit price in computing and statistics processing refers to the ratio of asked data that isn’t found inside the cache or reminiscence in comparison to the whole range of requests made. In different phrases, it measures the share of times that an asked piece of data isn’t to be had in the cache and needs to be retrieved from slower storage inclusive of the hard disk. In a caching gadget, the processor first checks its cache to see if the requested data is to be had. Fig 6:Shows Computation of Miss rate

Fig 6: Computation of Miss rate

If it isn’t determined, it is known as a cache leave out. The processor then has to retrieve the facts from fundamental reminiscence or disk, which takes a good deal longer. If the asked information is present in the cache, it’s far referred to as a cache hit, and the records may be retrieved quickly. The leave out price is vital because it without delay affects the performance of a computing system. An excessive miss charge approach that the processor is spending more time retrieving statistics from slower storage that could drastically slow down the general execution of a program. Then again, a low pass over rate means that most of the requested records are gift in the cache, leading to faster execution times.

Conclusion

The realization of this examine is that graph-based totally clustering via fast approximate matching is a good and correct approach for clustering large information. It can efficaciously take care of large datasets with a high range of dimensions and reveals right overall performance in phrases of both time and accuracy. Using approximate matching algorithms substantially reduces the computation time without sacrificing the nice of the clusters. Common, this technique cans significantly useful resource in organizing and reading big records and can be a precious tool for statistics scientists and decision-makers.

References

1. Manohar, M. D., Shen, Z., Blelloch, G., Dhulipala, L., Gu, Y., Simhadri, H. V., & Sun, Y. (2024, March). ParlayANN: Scalable and Deterministic Parallel Graph-Based Approximate Nearest Neighbor Search Algorithms. In Proceedings of the 29th ACM SIGPLAN Annual Symposium on Principles and Practice of Parallel Programming (pp. 270-285).
2. Oguri, Y., & Matsui, Y. (2024). Theoretical and Empirical Analysis of Adaptive Entry Point Selection for Graph-based Approximate Nearest Neighbor Search. arXiv preprint arXiv:2402.04713.
3. Geng, Y. A., Chi, C. Y., Sun, W., Zhang, J., & Li, Q. (2024). Disentangling Clusters from Non-Euclidean Data via Graph Frequency Reorganization. Information Sciences, 120288.
4. Li, J., Bian, H., Wen, F., & Hu, T. Knowledge Graph-based Diversity Analysis of Supplier Holographic Portraits. Applied Mathematics and Nonlinear Sciences, 9(1).
5. Liu, S., Wang, W., Zhong, S., Peng, Y., Tian, Q., Li, R., … & Yang, Y. (2024). A graph-based approach for integrating massive data in container terminals with application to scheduling problem. International Journal of Production Research, 1-21.
6. Xia, Y., Xu, Q., Fang, J., Tang, R., & Du, P. (2024). Bipartite graph-based community-to-community matching in local energy market considering socially networked prosumers. Applied Energy, 353, 122245.
7. Joo, Y., Choi, H., Jeong, G. E., & Yu, Y. (2024). Dynamic graph-based convergence acceleration for topology optimization in unstructured meshes. Engineering Applications of Artificial Intelligence, 132, 107916.
8. Uke, N. J., Lokhande, S. A., Kale, P., Pawar, S. D., Junnarkar, A. A., Yadav, S., … & Mahajan, H. (2024). Distributed privacy preservation for online social network using flexible clustering and whale optimization algorithm. Cluster Computing, 1-18.
9. Danielraj, A., Venugopal, P., & Padmapriya, N. Region adjacency graph based GNN approach for static signature classification. Journal of Intelligent & Fuzzy Systems, (Preprint), 1-18.
10. Putrama, I. M., & Martinek, P. (2024). Self-supervised data lakes discovery through unsupervised metadata-driven weighted similarity. Information Sciences, 120242.
11. Xue, X., Shanmugam, R., Palanisamy, S., Khalaf, O. I., Selvaraj, D., & Abdulsahib, G. M. (2023). A hybrid cross layer with harris-hawk-optimization-based efficient routing for wireless sensor networks. Symmetry, 15(2), 438.
12. Suganyadevi, K., Nandhalal, V., Palanisamy, S., & Dhanasekaran, S. (2022, October). Data security and safety services using modified timed efficient stream loss-tolerant authentication in diverse models of VANET. In 2022 International Conference on Edge Computing and Applications (ICECAA) (pp. 417-422). IEEE.
13. K. R. K. Yesodha, A. Jagadeesan and J. Logeshwaran, “IoT applications in Modern Supply Chains: Enhancing Efficiency and Product Quality,” 2023 IEEE 2nd International Conference on Industrial Electronics: Developments & Applications (ICIDeA), Imphal, India, 2023, pp. 366-371.
14. V. A. K. Gorantla, S. K. Sriramulugari, A. H. Mewada and J. Logeshwaran, “An intelligent optimization framework to predict the vulnerable range of tumor cells using Internet of things,” 2023 IEEE 2nd International Conference on Industrial Electronics: Developments & Applications (ICIDeA), Imphal, India, 2023, pp. 359-365.
15. T. Marimuthu, V. A. Rajan, G. V. Londhe and J. Logeshwaran, “Deep Learning for Automated Lesion Detection in Mammography,” 2023 IEEE 2nd International Conference on Industrial Electronics: Developments & Applications (ICIDeA), Imphal, India, 2023, pp. 383-388.
16. V. A. Rajan, T. Marimuthu, G. V. Londhe and J. Logeshwaran, “A Comprehensive analysis of Network Coding for Efficient Wireless Network Communication,” 2023 IEEE 2nd International Conference on Industrial Electronics: Developments & Applications (ICIDeA), Imphal, India, 2023, pp. 204-210.
17. M. A. Mohammed, R. Ramakrishnan, M. A. Mohammed, V. A. Mohammed and J. Logeshwaran, “A Novel Predictive Analysis to Identify the Weather Impacts for Congenital Heart Disease Using Reinforcement Learning,” 2023 International Conference on Network, Multimedia and Information Technology (NMITCON), Bengaluru, India, 2023, pp. 1-8.
18. Yadav, S. P., & Yadav, S. (2018). Fusion of Medical Images in Wavelet Domain: A Discrete Mathematical Model. In Ingeniería Solidaria (Vol. 14, Issue 25, pp. 1–11). Universidad Cooperativa de Colombia- UCC. https://doi.org/10.16925/.v14i0.2236
19. Yadav, S. P., & Yadav, S. (2019). Mathematical implementation of fusion of medical images in continuous wavelet domain. Journal of Advanced Research in dynamical and control system, 10(10), 45-54.
20. Yadav, S.P. (2022). Blockchain Security. In: Baalamurugan, K., Kumar, S.R., Kumar, A., Kumar, V., Padmanaban, S. (eds) Blockchain Security in Cloud Computing. EAI/Springer Innovations in Communication and Computing. Springer, Cham. https://doi.org/10.1007/978-3-030-70501-5_1